Decoding Player Submissions: identifying the best answers without knowing the right answer

08 Jul Decoding Player Submissions: identifying the best answers without knowing the right answer

In a previous blog post, we mentioned that the core of optimizing DNA sequence alignment was finding a reasonable trade off between maximizing the number of nucleotides that are correctly aligned, and minimizing the number of gaps. The goal of the alignment of two sequences is to group together the nucleotides they have in common in order to assess how similar they are, and eventually infer how related the organisms in which they were found are. Alignments are needed because sequences evolve over time, but the difference between two related sequences, even after millions of year of separate evolution, is still distinguishable from the difference between two unrelated sequences.

What are we doing exactly when we align sequences?

Even closely related DNA sequences eventually develop differences due to mutations that happen over time. So while there are specific proteins that we share with, say, chimpanzees, and work exactly the same in both organisms, their sequences are likely slightly different.

Most of the adaptation of species to their environment described by Charles Darwin actually consists of small mutation events that end up being positive in some environment, and the individuals with those mutations being favored in reproduction over thousands of generations.

Imagine a world where everyone spends 20 hours a day playing basketball and the most successful basketball players have the most children. Whenever a child is born abnormally tall, that child would tend to grow into a strong basketball player, and thus would tend to have many children. Tall people consistently having more children than short people would increase the average height of the population at each generation. This is exactly how giraffes became giraffes, over a really long time.

There are different types of mutations: a substitution occurs when a nucleotide is replaced by another. An insertion occurs when a nucleotide is added, and a deletion occurs when a nucleotide is removed. Substitutions will cause mismatches between related sequences, whereas insertions and deletions will introduce nucleotides do not map to anything (because they are new, or because their equivalent (homolog) does not exist anymore. We can model those as gaps.

But there are no hard rules as to how an alignment should be made since in practice all sequences have different characteristics. In other words, if we want to align TTCATAGC and CTTGACTG for instance, we have multiple choices.

And here we arrive at something that looks reasonable! A few gaps here and there, a mismatch, but it is believable that, a few thousand generations ago, those were the same sequence. We arrived at this result without enunciating generic rules, just by aligning things in a way that felt reasonable. Intuitively, we want to find a balance between maximizing aligned content and minimizing mismatches and gaps. It’s easy for humans to intuitively arrive at a compromise, but it is much harder to enunciate rules to teach how to do so to a computer, because there are many different “valid” solutions. There is no “right” answer.

How do we define a good solution when there is no “right” answer?

Let’s start from a much more down to earth example. Carlos, a coworker of ours, enjoys chicken a lot. He also likes getting a good bang for his buck, and is always looking for a deal. In his quest to get the best tradeoff between taste and price, he has visited most of the restaurants that sell chicken near McGill University in Montreal. He rated the quality of each meal out of 10.

Restaurant	Price ($)	Rating (/10)
A	8.50	8.5
B	12.00	7
C	5.00	5
D	18.00	9.5
E	11.00	7
F	7.00	4.5
G	10.00	7.5
H	13.00	8
I	14.00	9.5
J	8.50	5
K	10.00	8

Some restaurants are very easy to rule out. For instance, restaurants D and I offer pretty much the same plate, but I is cheaper, so Carlos, a conscious spender, never goes to restaurant D. Similarly, restaurant F is a cheap option at $7, but it’s not better than the $5 plate at restaurant C.

However, Carlos doesn’t have a strong preference between restaurant I and restaurant A. I is better, but A is much cheaper, so they both have their qualities. Neither is strictly worse than the other.

We can consider this in a more general perspective and define restaurants for which a strictly better alternative (both less expensive AND better quality) exists as “suboptimal”. Hence, the restaurants that are worse than no others can be considered “optimal”. The case where an option is optimal by virtue of not being strictly worse than any other option is known as Pareto optimality.

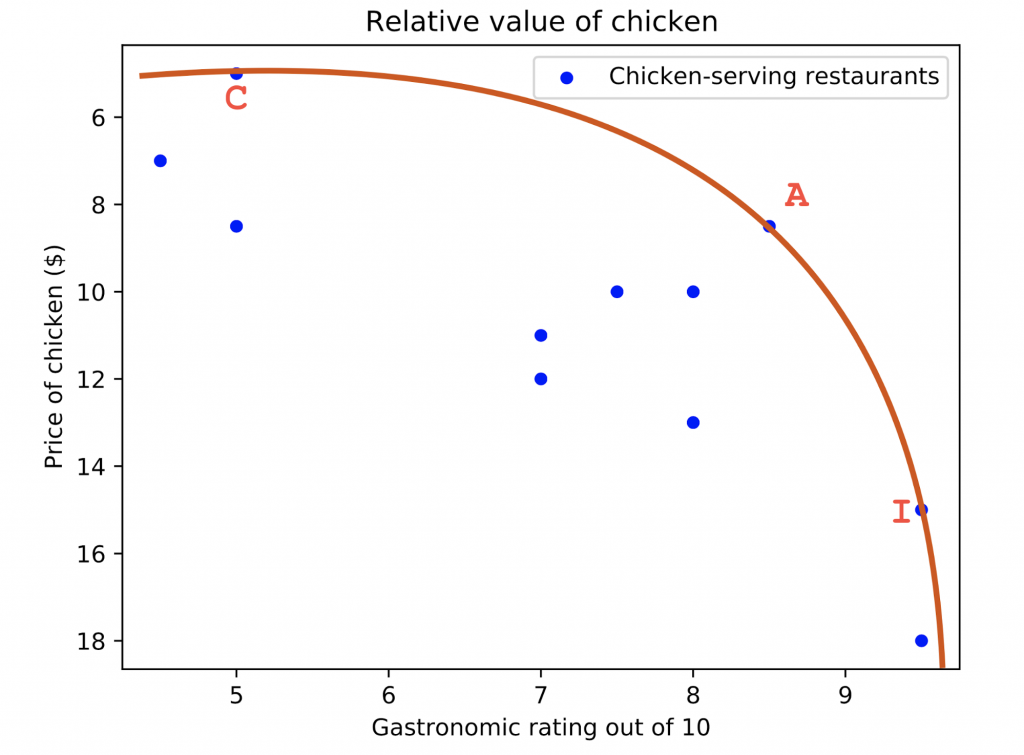
To visualize the problem, we can draw a plot of all the restaurants, organized by their performance on Carlos’s two criteria. We identify three restaurants that are worse than no others. We can define a line called the Pareto frontier, which is the set of points that are Pareto optimal. The nearer the line a restaurant is, the better it is as a lunch option.

Okay, but how in the world is this remotely related to Borderlands Science?

What we are doing with Borderlands Science is exactly the same idea; we are trying to optimize the tradeoff between maximizing the number of correctly aligned nucleotides, and minimizing the number of gaps. Thus, we are most interested in solutions that are not worse than other solutions. So, given all solutions provided for a puzzle, we can position them on a two-axis plot just like we did for the restaurants, and obtain data like the following:

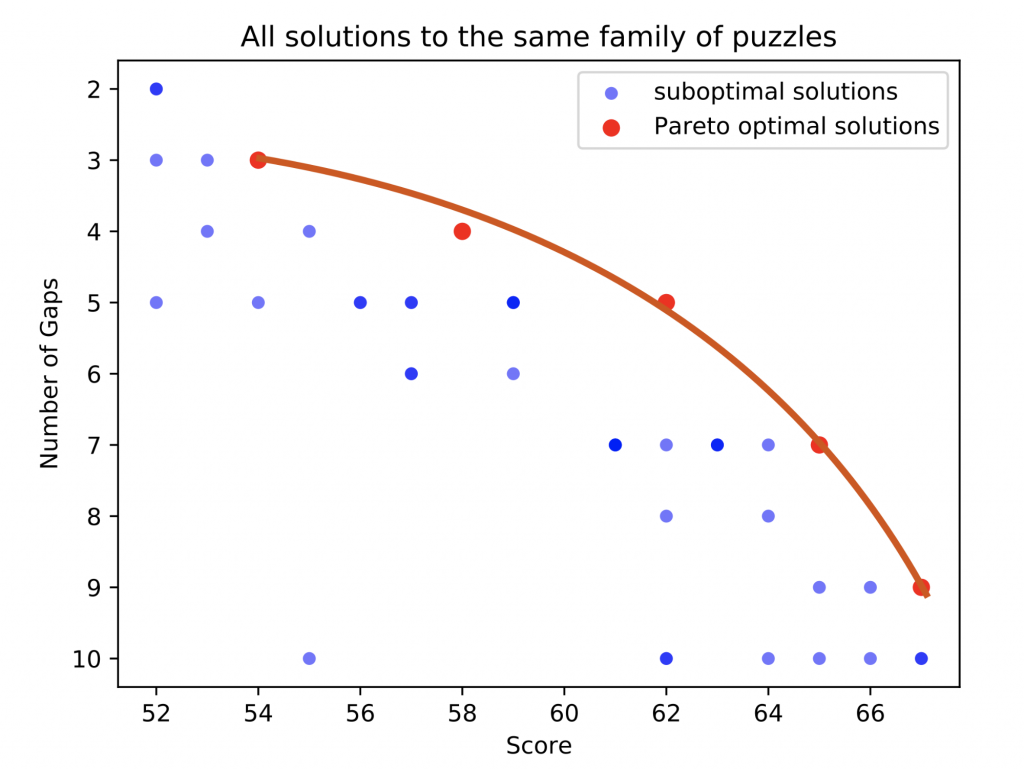
In order to assemble a new alignment, we use data from optimal or near-optimal solutions (near the red line). Note that on this plot of real data, darker blue points mean there are multiple solutions with the same score and number of gaps. As you see, there is a nice spread of different strategies for solving the problem; some players like to go fast and use the minimum number of tokens they can to get the par scores, and some like to fight for the high score. Moreover, not all players are given the same number of tokens to ensure we sample the whole solution space.

Thanks to this variety, we can obtain a good approximation of a consensus answer to the question “how do players intuitively address the tradeoff between score and gaps?”, based on submissions that are both varied and high-quality.